
要約統計量を用いて、データの全体像を把握しよう
マーケティングに関わっているのに、実は算術平均(Excelでいう=AVERAGE()です)とか加重平均しか知らない…という方、案外多いんです。 今回はそんなマーケティングの分析をワンランクアップさせる『要約統計量』についてのお話しです。webに限らず、マーケティングを行う上でデータの分析は必ず発生します。 そんなとき、この要約統計量を知っておくとデータの全体像を把握する上できっと役に立つはずです。
そもそも要約統計量とは?
要約統計量とは統計量の一種で、標本の分布の特徴を代表的に表す統計学上の値を指します(基本統計量、記述統計量とも呼ばれます)。 …これだけ言われてもよくわかりませんよね。 具体的に、どのような量を指すかといいますと、
- 平均
- 中央値(メディアン)
- 最頻値(モード)
- 分散
- 標準偏差
- 範囲(レンジ)
- 分位値
- 歪度
- 尖度
- 最大値
- 最小値
- 要素数
などが挙げられます。 今回は、特に以下の5つの量に注目してみましょう。
- 最小値
- もっとも小さい値
- 第1四分位値
- 小さい方から数えて25%の位置にある値
- 中央値(第2四分位値)
- 小さい方から数えて50%の位置にある値
- 第3四分位値
- 小さい方から数えて75%の位置になる値
- 最大値
- もっとも大きな値
たとえば、
10 25 8 19 20
という十個の数値があったとき、これを小さい順に並び替えると、
8 10 19 20 25
となります。この場合に、先ほどの量は以下に該当します。
- 最小値
- 8
- 第1四分位値
- 10
- 中央値
- 19
- 第3四分位値
- 20
- 最大値
- 25
となります。図で示すとすれば下記のようなイメージです。
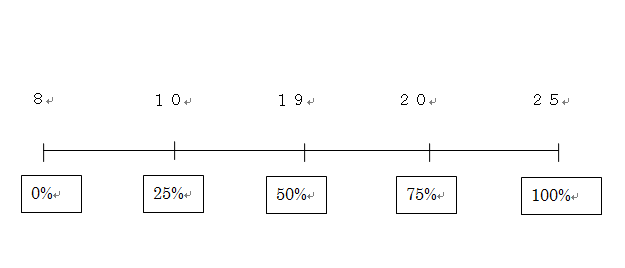
要約統計量の使用例
たとえば、次のようなデータがあったとします。
| No | 日付 | imp | click |
|---|---|---|---|
| 1 | 4月1日 | 139 | 13 |
| 2 | 4月2日 | 40000 | 510 |
| 3 | 4月3日 | 101 | 21 |
| 4 | 4月4日 | 162 | 19 |
| 5 | 4月5日 | 172 | 29 |
| 6 | 4月6日 | 87 | 4 |
| 7 | 4月7日 | 501 | 29 |
| 8 | 4月8日 | 145 | 13 |
| 9 | 4月9日 | 191 | 12 |
| 10 | 4月10日 | 294 | 15 |
| 11 | 4月11日 | 129 | 15 |
| 12 | 4月12日 | 153 | 21 |
| 13 | 4月13日 | 188 | 3 |
| 14 | 4月14日 | 161 | 22 |
| 15 | 4月15日 | 150 | 13 |
| 16 | 4月16日 | 120 | 14 |
| 17 | 4月17日 | 244 | 18 |
| 18 | 4月18日 | 114 | 7 |
| 19 | 4月19日 | 135 | 12 |
| 20 | 4月20日 | 138 | 11 |
| 21 | 4月21日 | 91 | 5 |
| 22 | 4月22日 | 149 | 10 |
| 23 | 4月23日 | 105 | 6 |
| 24 | 4月24日 | 151 | 2 |
| 25 | 4月25日 | 226 | 13 |
| 26 | 4月26日 | 190 | 3 |
| 27 | 4月27日 | 185 | 19 |
| 28 | 4月28日 | 137 | 8 |
| 29 | 4月29日 | 148 | 12 |
| 30 | 4月30日 | 131 | 11 |
Imp数について、単純に平均を考えてみると、
平均 = (139+40000+101+・・・+137+148+131) ÷ 30 ≒ 1494.6
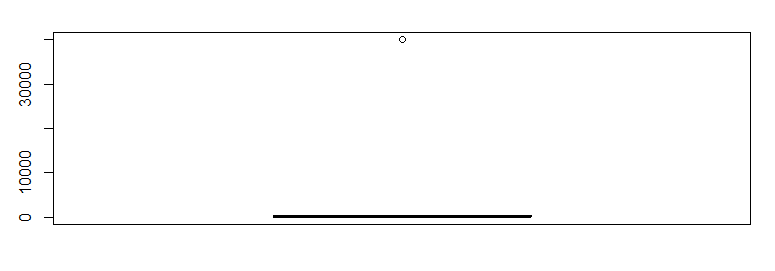
となります。しかし、グラフを書いてみると、以下のようになります。

平均値は、明らかにこれを「一日当たりのクリック数」として利用するのは不適切だとわかります。ここで、上記5つの要約統計量をそれぞれ計算し、
- 最小値
- 87.0
- 第1四分位値
- 132.0
- 中央値
- 149.5
- 第3四分位値
- 187.2
- 最大値
- 40000.0
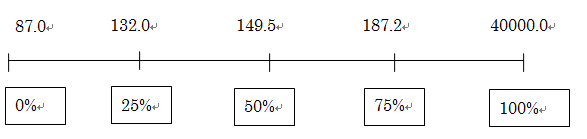
これを図(箱ひげ図)に表してみます。
こうすることで、平均値だけを追っていても、なかなか見えてこなかった様子がとらえられました。 つまり、
- ①上部に飛び出ている値(40000)は外れ値だと思われる。
- ②下の方にデータが偏っている。
などの特徴が読み取れるかと思います (「87.0~187.2」周辺までが、データ全体の75%を占めているイメージです)。
この外れ値が邪魔であれば、これを除外して平均を計算してみたり、再び図を書いてみたりして見ましょう。
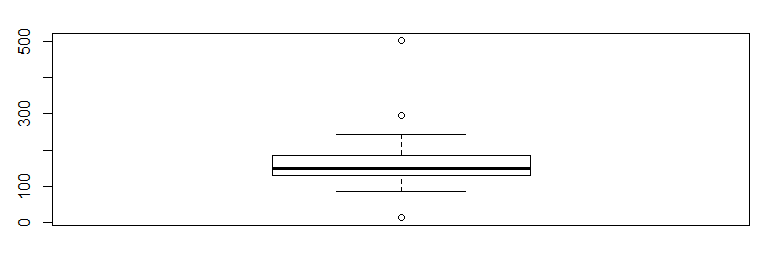
このように、一つ一つ順番を追って、データの特徴を追ってみると、今まで見えてこなかった特徴が追えるかと思います。 他の量、歪度や尖度、分散などについても、色々計算を行い、様々な角度から特徴をとらえてみてください。
補足
今回は、外れ値を検出する際、図を書いて目視により調べていました。
※イメージ
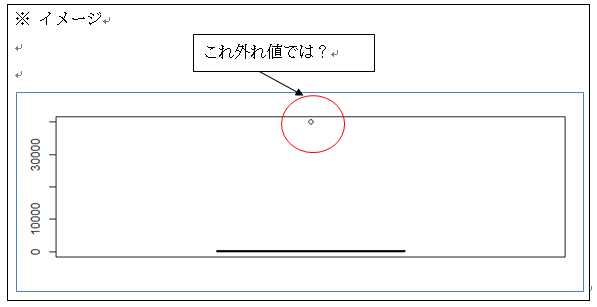
これ以外にも、仮説検定によって外れ値を検出する方法もあります(「Smirnov-Grubbs検定」「Dixon検定」など)。興味がある方は、こちらも調べてみると良いでしょう。
要約統計量のまとめ
平均値を求めることでデータの全体像をつかむ第一歩とはなりますが、この値だけでは外れ値に弱く、誤った結論を導いてしまう可能性があります。他の要約統計量を合わせて使うことにより、様々な角度からデータの特徴をつかむことができるので、データ分析に携わる方は身に着けておいて損はないです。